オセロでこのカウンティングとは…
文字通り数えること!
それだけです(’-‘)ノ
- 序盤は少なく、中割りを意識する。
- オセロは打てる箇所数が多い方が有利になりやすい。
- 隅(角)は狙う!
など色々な戦術があるのですが、
特に終盤の2~4マス空きくらいに差し掛かると、
如何に沢山石を残すか?
これが非常に大事になってきます。
特に僅差の終盤となった時は、
- しっかり数えて正しく打ったことで2石勝ちできた
- 適当に打ったら2石負けした。正確に打っていれば勝ててた
と言う結果になることも多いです。
考え方自体は非常に簡単なので身に付けておこう。
2マス空きの場合のカウンティング
まずは最も簡単な例題、2マス空きです。
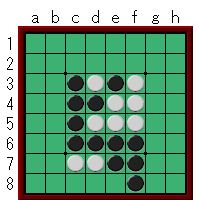
こんな局面。
貴方は黒の立場です。

終局までの打ち方は、
- 黒a7→白a8
- 黒a8→白a7
この2パターンです。
それぞれ考えてみましょうか。
黒a7から打つ場合
現状、黒は29石あります。
ここでa7に打つと、返す石は上、右上、右の3方向。
- まずは着手した石も加算されるので+1
- 上方向は4石
- 右上方向は1石
- 右方向も1石
全部で7石取れます。
次は白です。
ここで、a列は全部黒になったので、こちらは白には取られません。
また、相手の着手した石自体は、これで黒の数が減るわけじゃないので、カウントしなくてOk。(わりと重要)
黒が白に返された分だけを数えましょう。
白に返される石数は…
- 右上方向に1石
- 右方向に1石
合計2石です。
つまり最初29石、黒a7で36石、白a8で最終的に黒は34石になり、勝ちです!
黒a8から打つ場合
同じように数えてみましょう。
黒a8によって取れる石は…
- 着手した石で1石
- 取るのは右上方向のみで2石
合計3石です。
次に、白はa7によって取られてしまう石数を数えます。
返す石は右方向のみで2石です。
結果、黒は29+3-2となり30石になります。
残念ながら負けです。
つまりこの局面では黒a7が正解になります。
問題のためにわざと設定したようにも見えますが、
黒隅(角)を取ると負けてしまいます。
このように終盤は隅(角)を取れば負けるようなケースが珍しくないです。
特に2マス空きまで来れば、数えれば簡単に分かると思うので、必ず数えるようにしよう。
3マス空きの場合のカウンティング
では少し難易度を上げて、3マス空きのケースです。
貴方は白の立場です。
どこに打つと良いでしょうか?
これも打ち方の総数は
- 白f1→黒g1→白h1
- 白f1→黒h1→白g1
- 白g1→黒h1→白f1
- 白g1→黒f1→白h1
- 白h1→黒g1→白f1
- 白h1→黒f1→白g1
この6通りが存在します。
とりあえず、現段階ではこの6通りにおいて数えてみましょう。
難しかったら、上盤面の「Put」をタップして見てください。実際に打つことができるようになります。
では結果です。
まずは、現状の白の石数を数えておきましょう。
全部で25石あります。
この時点で、勝つためには33石以上、つまり最低でも8石は取らないといけない。
ってことを念頭に置いておくと良いでしょう。
(白→黒→白と打って8石差を埋めないと行けないので、結構取る必要があります。)
では、実際に数えてみましょう。
- 白f1→黒g1→白h1 →白34石(勝ち)
- 白f1→黒h1→白g1 →白35石(勝ち)
- 白g1→黒h1→白f1 →白32石(引き分け)
- 白g1→黒f1→白h1 →白31石(負け)
- 白h1→黒g1→白f1 →白29石(負け)
- 白h1→黒f1→白g1 →白32石(引き分け)
白の1手目が区別しやすいように色分けしました。
白の1手目に対して、黒は石が多く残る方に打つ前提と考えるべきで、
この場合白はf1に打つのが正解です。
黒どちらに打ってきても白の勝ちです。
他の白初手g1、h1は黒に正しく打たれると負けます。
それ以上の空きの場合は?
では4マス空きになったらどうなるのか?って話です。
一応、全ての空きに打てるものと仮定すると、打ち方のパターンは全部で24通りになります。
これは4の階乗に相当するんですね。
(高校数学で習ったと思います。文系も習ったと思います 爆)
4マス空きでの打ち方は4通り
次は3マス空きになるので3通り
続いて2マス空きになるので2通り
最後は1通り
4マス空きならこれらを全てのパターンとなるため、4×3×2×1=24通りとなります。
同じように計算していくと…
- 5マス空き:5×4×3×2×1=120通り
- 6マス空き:6×5×4×3×2×1=720通り
- 7マス空き:7×6×5×4×3×2×1=5040通り
- 8マス空き:8×7×6×5×4×3×2×1=40320通り
はて、これ全部数えるの?
まず無理ですよね。日が暮れます。
先の話にはなるんですが、有段者レベルだと、局面にもよりますが6~8マス空きくらいなら、正確に打ってくる人も普通に居たりします(笑)
じゃあ、本当に40320通りも全部読んでらっしゃいますの??
ってなるんですが、そんなハズはありません。
では、ちょっとこの局面を見てみましょうか?
貴方は白の立場です。
白f1に打ってみました。
次黒番ですが、黒はh1に打つことが出来ず、g1しか打てません。
つまり、白1手目でf1に打つと、その後は黒g1→白h1の1通りしかないんです。
さらに、白初手h1に打つと…
この場合も黒はg1しか打てません。
白1手目でh1に打つと、その後は黒g1→白f1の1通りしかないんです。(この場合2石負けになりますが。)
白初手g1の場合は2通りあります。
3マス空きの局面ですが、このように打てない場所と言うのも結構あります。
上で示した【空き数】の階乗というのは、あくまで最大数であり、通常はそれより少なくなることが多いです。
明らかに論外な場所が結構あるよ
流石に2~4マス空きくらいの終盤になったら、上のように一つ一つ数えた方が良いことも多いですが、
8マス空き程になると、まだまだ手筋で考えるべき局面と言うのも多いです。
この辺は、これから先、色々な打ち方を身に付けて行くと、しぜーんと身についてきます。
「明らかに無い」と言う着手場所も割とあるので、8マス空きだからと言って40320通りも数えないといけない。
なんてことはそうそうないでしょう。
現状はとりあえず、2~3マス空きくらいは損しないようにしっかり数える。
ってことを実践すれば大丈夫です!

コメント