名づけたのはσ(・・)ではないですよ?
ここまで色々な中割りについて触れ、
返した石が綺麗に囲まれているとか、むき出しになっているとか散々言ってきました。
ここでは、着手の良し悪しを見た目ではなく、
具体的数値に置き換えて判断する、若干理系的な考えで打つ方法です。
難しそうな名前が付いていますが、考え方はそれほど難しくありません。
ここの内容はある程度オセロに慣れてきたら、それほど重要ではありません。
ってか、無駄に計算することなく一瞬で分かるようになる。
なので参考程度に読んでみてくださいな♪
目次(もくじ)
空いている数を数えてみる
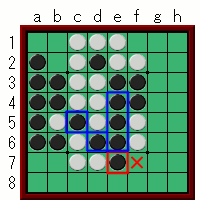
では早速ですが、次の局面を見てみよう。
貴方は白の立場です。
今回は①のf3、②のe2、③のc1に打つものとして、それぞれの解放度を考えてみよう。
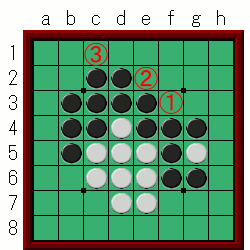
開放度はどうやって求めるのか?ですが…
各石の周囲1マスに空きが何個あるかを数えて、数値化する。
1つの石を数えられたら、複数の石を返す場合は2つめの石も同様に数える。
全ての石について数値化できたら、最後に合計する。
この合計したものが解放度と言います。
実際に上の①②③についてやってみよう。
①のf3については…
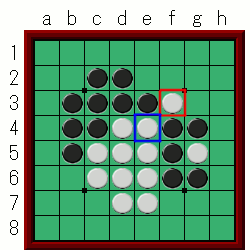
返した石はe4の1石のみ。
e4の周囲を見ると、空きマスは…無いですね。
この場合は解放度は0になります。
②のe2については…
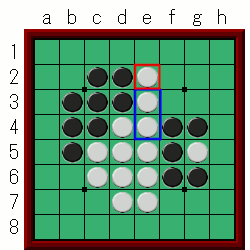
返した石はe3、e4の2石です。
まずe3の周囲の空きますを数えると…2ですね。
次に、e4の周囲の空きますを数えます。1になります。
この2つを合計、2+1で解放度は3となります。
初心者の打つ大量取り
次は、初心者の典型的な「最初から大量の石を取る」人的な打ち方。
c1に打ってみます。
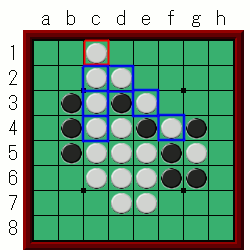
返す石は、c2、c3、c4、d2、e3、f4
と6個も返します。
これも同じように1個ずつ、周囲の空きマスの数を数え、解放度を出していきます。
- c2:3個
- c3:1個
- c4:0個
- d2:3個
- e3:3個
- f4:2個
つまり、3+1+0+3+3+2で解放度は12にもなります。
開放度的にどこが最善?
で、結論を言えば…
解放度は0が最小で、数値が小さければ小さいほど好手になりやすいです。
今回の例では、

f3に打つ場合ですね。
当サイトでは、返した石が綺麗に囲まれている中割りは好手と説明してきましたが、
綺麗に囲まれている=解放度0と言うわけです。
当然解放度が大きい程悪手になりやすいです。
上の例で言えばc1に打った場合ですね。

返した白の周囲は空きますだらけであり、黒はここに沢山手数ができました。
繰り返し言いますが、オセロは打てる箇所数が多いほど有利になりやすいゲームであり、
白のc1のような手は黒を有利にしてしまう=自分が不利になるわけです。
解放度は毎回数えないとダメ?
実戦では数える必要はないですね。
数えていたら流石に時間が掛かりすぎるので。
中割りしてみたけど、本当に良い手かどうかを検証したい時に、数値で考えてみるのも良いかも知れませんね。
あくまで理論ということで(´ω`)
とりあえず、ここまで色々な中割りをやってきました!
ざっくり練習問題を作ってみたのでお手隙でしたらやってみてください。

コメント